Binary Classification using Decision-Tree Model

12 min readMay 16, 2021

Welcome readers.

Introduction to the problem :- In this blog, I would like to help you guys to build a Machine Learning model based on the Decision Tree Algorithm. Here, we shall be working on a smaller dataset of diabetic people. We shall first be training our model using the given data and then shall be performing the Binary classification using the built model.

Fundamentals :- Here our main agenda is to identify, which is going to be the root-node and what would be our splitting criteria for further level-nodes. We can use, thus formed Decision-Tree (If-else based rule-engine) in order to perform the classification for any new incoming data. Tree-depth plays a crucial role in deciding whether the tree is over-fitted or not ?

Data-Exploration & Domain Understanding Phase :- First, let’s begin by importing the dataset into our Jupyter Notebook :-

Next, we can investigate the data-types of each of the attribute(aka feature) in the given dataset. Please note here that, in-total we have been given 9 features out of which, given to us are 8 independent variables and “outcome” attribute is our dependent variable. The outcome value as 0 indicates that, person is NOT diabetic AND the outcome value as 1 indicates that, person is very well diabetic. So, the “outcome” for us is a categorical (i.e. Binary) type of variable. From the below data-set, we can note that, there are around 768 rows in the data-set and 9 columns.

Next, let’s see how many rows for each of the variable have the NULL values :-

Let’s load the data first and see how does it looks like :-

Next, we may want to change the title of the some of the columns, so as to fit in our requirements. Let’s propose the changed names of the columns as per our own discretion. This is entirely optional step.

Below is how the new data looks like with changed headers/titles :-

Next, let’s check how many number of users have Diabetes AND how many don’t have Diabetes :-

Also, let’s check the same aforesaid data in terms of percentages of users have Diabetes. Below data indicates that around 65% of users have diabetes and 34% don’t have diabetes.

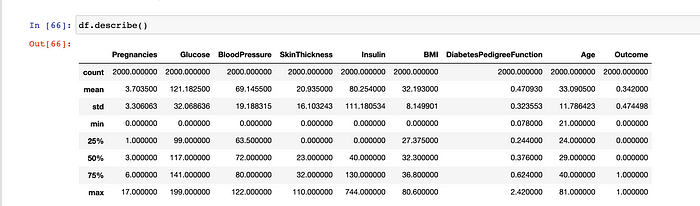
Let’s list down statistical summary of all features in our data-set. ‘‘describe” is a very Important function to see the statistical information. Please note that, it makes sense only for Continuous/Numerical variables like BP, Skin-Thickness only. It doesn’t makes any sense for Nominal or Ordinal variables. From below data for BP, there are 768 records in total in this data-set and mean BP is around 70 with Std-deviation of 19. The maximum BP observed is 122.

Let’s now see the histogram view of the the ‘ BP’ feature from the given dataset.

Similarly, we can also see the histogram view for all the features at once, in the given input data-set :-

Next, let’s see in the given data-set, how many records have diabetes and how many users don’t have diabetes at all. This data-set seems to be imbalanced. We might have to do some sampling approach, but for now, let’s skip it.

Next, let’s plot a pair-plot relationships in this dataset. By default, this function will create a grid of Axes such that each numeric variable in data will by shared across the y-axes across a single row and the x-axes across a single column. The diagonal plots are treated differently: a univariate distribution plot is drawn to show the marginal distribution of the data in each column. For example, the left-most plot in the second row shows the scatter plot of ‘Glucose’ versus ‘Pregnancies’.

Next, let’s perform a correlation analysis between the features themselves. Usually, a value of 0.7 and above is considered as a good value and indicates that there is a high co-relation between those features. For e.g. the highest correlation for our given data is between ‘Pregnancies’ and ‘Age’ attributes.

Outlier treatment :- Next, let’s see the box-plot summary of the entire dataset. From the below data, its evident that lot of people have too high (outlier) value for Insulin.

Also, lets observe the box-plot summary for each attribute wise as well :-

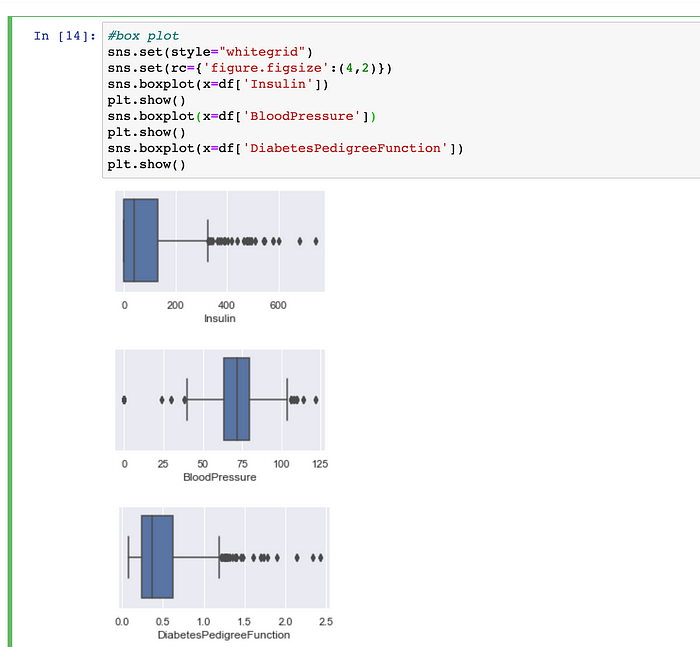
Next, since all of our attributes are numeric type, we can very well treat these outliers. Let’s first find out the range of each of the attribute .

From outlier-formulae detection for numeric/continuous attributes, we know that for any attribute, if it’s corresponding value lies outside of the following range : [(Q1–1.5 * IQR), (Q3 + 1.5 * IQR)], then that records would be considered as an outlier. Let’s first find out the range for each of the continuous attribute with aforesaid formulae. For example, from below demonstration, its visible that, for attribute ‘BMI’, the normal range is (13.2375, 50.9375) — Any record having value for BMI attribute outside this range shall be considered as an Outlier.

Let’s revisit the original data-frame once. From below demonstration, its clear that, we have in-total 2000 records and from all the given records, the range of BMI given to us is : <0, 80>. So, there shall be some records, who would have value of ‘BMI’ as 0 and some records would also have value for ‘BMI’ as 80. These shall be outliers obviously. Similarly there would be some records having outliers in other attributes as well.

Let’s now remove the outliers from our original data-frame. We would be now left with 1652 records. Remember that, originally we had 2K records. Also note that, in the data-frame (which is free from outliers), the range of ‘BMI’ is <18.72, 50.70>. Remember that, originally the normal range of ‘BMI’ was (13.2375, 50.9375).

Next, let’s again plot a pair-plot relationships in this dataset. With the below visualisation, we can say that some part of the pre-processing has been done for the given data-set.

Building ML model Phase :- First, let’s begin by dividing the given data-set into features and target variables. Please note here that, ‘X’ contains all of our independent-variables/features AND ‘y’ contains all of our dependent variables. In other words, ‘X’ represents the input variables and ‘y’ represents the output variable.

Let’s observe whether our data got divided into the same or not :-

Next, lets divide the given data-set amongst training & test data-set. First, let’s understand what is meaning of train & test data. Training set — a subset which is used to train a model. Test set — a subset used to test the trained model. We have used the library ‘sklearn’ for this very purpose. Please note that, we have spliced the data in the ratio of 80% i.e. (80% of 1652 ie. 1321) shall be used for training purpose and remaining 20% (20% of 1652 ie. 331) records shall be used as test-data. We have also specified here the ‘random_state’. It stands for Reproducibility. For e.g. It may happen that, next time when we run this sampling again, different rows may land up in test & train dataset. So, If I decide the value for ‘random_state’ now and keep it constant, then every time we execute this statement, same set of rows shall be picked up and bifurcated into train & test dataset.

Building model using ‘Entropy’ as the criteria :- Next, we shall be using the DecisionTreeClassifier from the sklearn.tree library provided by python. Please note here that, DecisionTree based model can be used for both the purposes i.e. Classification & Regression as well. In the context of this problem, here we are performing the task of Binary classification. We therefore fit into the model the training & test dataset AND finally, we do prediction on the testing dataset. From below observation, please note that, ‘y_pred’ indicates the predicted results (on the X_test data) by our newly-learnt model. Also remember that, ‘y_test’ is the original-actual-given value of the label for our test-data set.

Evaluating Model’s Performance Phase :- First, let’s begin by importing the libraries for getting to see the metrics from ‘sklearn’ and thus, we can see the accuracy of our model on the test-data :-

Similarly, let’s see accuracy on the training dataset. Since model has learnt from the train data only, obviously the accuracy on the train-data would be 1.

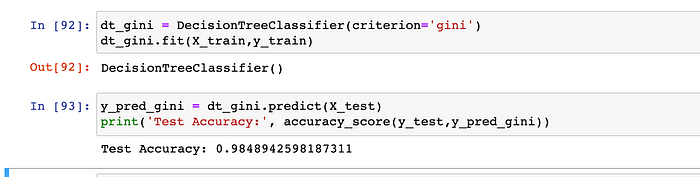
Building model using ‘Gini’ as the criteria :- Let’s try with ‘gini’ as the criteria for our DecisionTreeClassifier. We can easily observe that, the accuracy has increased to 98.48 % as well.

Let’s now see the confusion matrix for the ‘y_test’ (i.e. the actual values of the outcome) & ‘y_pred_gini’ (i.e. the predicted values by our model).

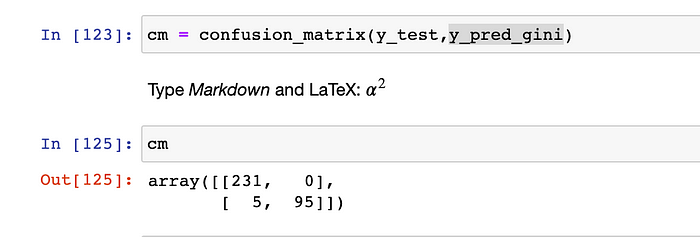
Confusion-Matrix is a 2*2 grid / matrix which demonstrates the performance actually. Above 2 * 2 grid can be considered as following table :-

True-Positives → These are such records, which originally have the outcome as TRUE and these are predicted as TRUE (by our model) as well. We have 231 such records. From below demonstration, its evident that in the test-data, there are 231 records having label as 0 & 100 records having label as 1.

From below demonstration, its evident that in the predicted-labels from the test-data, our model predicted 236 records as having label as 0 & 95 records having label as 1.

False-Positives → These are such records, which are originally having outcome as FALSE, but our model have predicted them as True. We have ZERO such records, which is a good indication.
False-Negatives → These are such records, which originally have the outcome as FALSE, and our model have predicted these records as FALSE too.
True-Negatives → These are such records, which originally have the outcome as TRUE, but our model have predicted these records as FALSE. There are 95 such records. (i.e. For these 95 records, ).

Now, The Accuracy alone may not be the correct identifier for any ML model. We have many other KPIs to find the performance of the model. All of the below parameters would tell us, how good our model is :-

Precision [TP / (TP + FP)] is the ability of the model(classifier) of not labelling a sample as positive, which is actually negative. In other words, out of all the positively predicted classes, how many are actually positive.

Recall [TP / (TP + FN)] is intuitively the ability of the classifier to find all the positive samples. In other words, out of all positive classes, how much we predicted correctly. This should as high as possible.

F1-score (i.e. F-measure) [(2 * Recall * Precision) / (Recall + Precision)] can be interpreted as a weighted harmonic mean of the precision and recall. This is a balance between recall & precision.

Support :- It indicates about the number of records in the test-data-set with class as 0 (Non-diabetic) and class as 1 (Diabetic).

Macro-Average :- It indicates the average precision, when we consider two different splits of the data. For both of those splits, we calculate the average precision & recall. For example, in order to compute the macro-average-value of precision → [(P1 + P2) / 2]. Similarly, for computing the macro-average-value of recall → [(R1 + R2) / 2].

Weighted-Average :- For example, in order to compute the micro-average (i.e. Weighted average) value of precision, following formulae can be used → [(TP1 + TP2) / (TP1 + FP1 + TP2 + FP2)].

From above figure, we can observe that, for class-1 (i.e. Diabetes==TRUE), the precision is 100% and recall is 95%. It can be considered as a very good model.

Next, we know that in every Decision-Tree based algorithm, objective is to find out which would be the best root node and so on. We do so on the basis of Entropy / Information-Gains and select the best node. Let’s visualise the model constructed by aforesaid library for our use-case. We can see that, our tree looks too dense.

Model optimisation Phase :- Let’s now optimise our model by decreasing the level and complexity. We shall be limiting the depth of the tree to 4 only. Higher the depth of the tree, higher would be chances of over-fitting.

Next, let’s again prepare the decision-tree model and perform the prediction.

Now, the performance of the model seems to be standing at 72%. It might improve, depending upon the

The final model now also looks more slim & trim :-

We can also observe that which features are most important in deciding the label (i.e. whether person shall be diabetic or NOT) :-

Consuming the Model for prediction :- Let’s see to predict the output (whether person shall be diabetic or not) basis upon some random input-data-row. Let’s pick up any random row from our given data-set :-

Next, let’s prepare the input-data for our model from above random record by dropping the output variable (i.e. dependent variable) and one of the unrelated independent variable (ie. skin) :-

Now, we perform the operation of binary-classification using the optimised ML model. We observe that, our model is predicting the label as 1 and also the actual label is also 1.

Conclusion :- Please note that, Decision-Trees can also be used where dependent-variable can have values from some given range as well, not necessarily binary always (i.e. Multi class classification).

References :-

Binary Classification using Decision-Tree Model

Written by aditya goel